Hex Editing for Archivists (Part 1)
Basic Introduction
Table of contents
Abstract
In this tutorial, I'll explain what a "hexadecimal" numeral system is, why it makes sense to use it for bytes (=data), and how to use a "hex editor" to view and edit binary data. Just simple examples, not going to hack the Pentagon or anything.
This article is mainly aimed at archivists with digital preservation needs, and maybe a bit for data forensic beginners.
There is also a PDF version of this document available for download, as well as its Markdown source code.
What is "Hex"?
The term "hex" is short for "hexadecimal". Long story short: In the western world, most of us only have to deal with one numeral system: The decimal system. Thanks to our fingers and toes, the base of this numeral system is 10.
So we only need 10 different numbers to count: 0 - 9, and we add more positions the higher the number gets: 1, 22, 333, 4444, ... and so on.
But what if we'd have a different base than 10? Let's use the number 16 as base. Hexadecimal means: hexa=six and deci=10. Sixteen. I'll explain later why that number.
So for a hexadecimal system, we need more characters to be able to count beyond 9 before incrementing the number of digits. Some smart engineers came up with the idea of using the letters A to F.
Oh, btw: it's common to write hex-numbers prefixed with "0x". So "0xF" would be the number 15 in decimal.
That's because counting in hexadecimal now goes like this:
- 0 = 0x0
- 1 = 0x1
- 2 = 0x2
- 3 = 0x3
- 4 = 0x4
- ... you get the idea ...
- 8 = 0x8
- 9 = 0x9
- Now it gets interesting:
- 10 = A
- 11 = B
- 12 = C
- 13 = D
- 14 = E
- 15 = F
Now, why only 15 when the base is 16? Well, why only 9 when the base is 10? Same reason :) (That's me cheating me out of a proper mathematical answer... Sorry. You'll have to ask your former math teacher)
Anyways. Why is base 16 useful for handling digital data? Because one byte is 8 bits, and 2^8 (=the highest number that can be depicted using 8 bits) is: 255 So one byte can count from 0 to 255.
Applying your newly aquired "hex-foo", try to count to 255:
- 0x00 (You need 2 digits now, because 255 > 15 (=0xF)
- 0x01
- 0x02
- ...
- 0x0F (=15d)
- 0x10 (=16d)
- ...
- 0xF9 (=249d)
- 0xFA (=250d)
- 0xFB (=251d)
- ...
- 0xFF (=255d)
Beautiful, isn't it? Now displaying any value of one byte only uses 2 digits (instead of 3). And best of all: Each digit is half of the byte = 4 bits. The lower and the upper 4 bits. Such a "half-byte" is called a "nibble" btw. Don't know why. Ancient Nerd-History.
As an experienced developer, who has to deal with bit-patterns in a byte quite often, you "know" the bit patterns for 0 to F. It's like the multiplication table we all learn as kids. Once you got it, it's "just there".
I hope it's a bit clearer now why "hex" is awesome for handling bytes.
Hex Editor: Basics
Just like a plain text editor - which can only be applied to read plain text, there are editors for viewing (and editing) binary files.
Have you ever opened a binary file, let's say a ".exe" or ".bin" or ".dat" file in a text editor?
Looks like someone puked a random set of ASCII characters all over a white page.
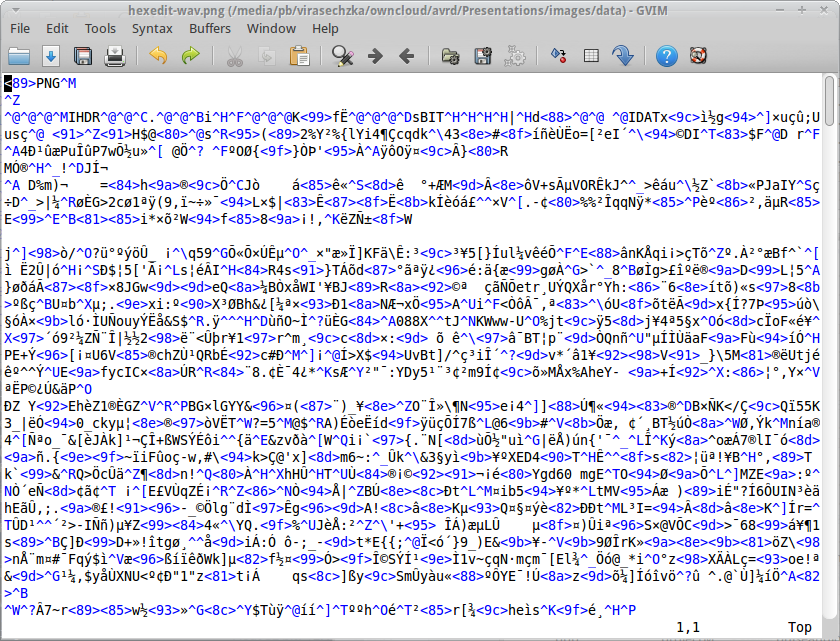
Character chaos: Opening a binary file in a text editor
That's because the text editor tries to "understand" the bytes as text characters.
Sometimes it may even crash your editor, because some of these characters are "magic" when output as text. My favorite "control character" as a kid was ASCII No. 7: Bell.
You echo that character on the screen, and nothing appears - but the PC beeps. Others, more well known ones are:
- Spacebar = 0x20
- Line Feed = 0x0A
- Tab key = 0x09
- Backspace = 0x0D
Here's a more detailed list of ASCII control characters as a reference. It's not required at all for this tutorial, but maybe interesting - in case you're curious :)
That's why we need a special editor to view binary files. One that does not try to "understand" the data, but rather shows it as-is.
Visual Layout
Now, the basic layout of a hex editor is usually divided into 3 columns:
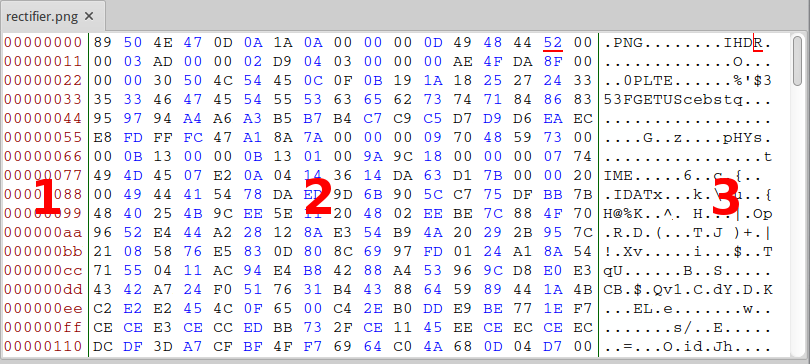
The 3 columns of a hex editor
- Data position
- Binary data in hex
- Binary data in character encoding (e.g. ASCII, ...)
When you open a binary file, like an image (JPG, BMP, PNG, ...) or a WAVE file (WAV), or even an executable (those are files that you can execute/run. Those are your "programs" or "applications". They contain the viruses ;)): You might recognize the random ASCII chars from the poor white page. Yes, the right column is what the bytes would be rendered as text.
As mentioned before, some characters are "magic" and don't have a graphical representation. They're called "non printable chars". Most hex editors substitute these "NPCs" by dots "." so you can more easily keep track of which character position you're looking at.
How many bytes you see per row, is usually something you can configure in the editor's settings. I'm used to working with about 16 or 24 bytes per row. If I use more, I feel it's easier to lose track of the byte position I was trying to follow or relocate. However, sometimes it may be beneficial to increase that number. If you feel you lose your way in the "field of data rubbish", try to decrease the number of bytes per row.
Some hex editors auto-resize this number depending on the window size. If you like to work full screen, but the bytes-per-row number is too high, try increasing the text size. That'd be your first "hack" ;)
Reading, analyzing the data
You will see your cursor somewhere. Not your mouse cursor, but a text cursor that usually blinks or highlights a position in the text. The whole display area of the data within the hex editor is just text.
There should be 2 positions highlighted. They both show the same position in the file, but in 2 different views:
- One in the hex column
- One in the text column
In order to choose whether you want to edit the data by their hex value or its text character representation: you can jump between the hex and the text column.
Very often this is done using the "tab" key. The tabulator (2 arrows, on the left side of our keyboard). Hitting it toggles your editing position back and forth between hex and text.
Let's go through the 3 columns from left to right:
Data position
Usually 8 hexadecimal digits. They represent the byte position, the so called "offset" showing you where the row of bytes is located within the file. If you move your cursor around on the data bytes, you'll often see your offset shown for easier locating.
For easier reading, the 8 digits are sometimes split with a colon ":". Looks like this:
0001:000F
Which would be: 0x1000F = 65551 in decimal. You're at byte #65551 in the file. You only need one "coordinate" for navigation in a file: it's just one long stream of numbers.
When you want to go to a certain position in the file, there's usually an option like "goto offset" - very often the keyboard shortcut "Ctrl+G".
In specification documents, in order to navigate to different structural parts in the file quickly, give you their data offset information.
Binary data in hex
The middle column is the binary data as-is. Uninterpreted and just displayed byte-per-byte as a hex pair. If you see a "00" it means the number 0. If you see "FF" it's a full byte: 255.
That's pretty much it.
Binary data in character encoding
Here you see each byte interpreted as a text character. Which text you'll see depends on the "character encoding": How numbers are mapped to chars. Non-printable characters are often displayed as dots "." - so it's easier to keep visual track when following byte positions.
Some numbers are interpreted as alphanumeric characters. Don't be confused: They are not real "text", but mere random characters. Their byte data is encoded numbers, so they are not meant to be displayed as characters. That's what makes viewing binary files as text so weird.
However, sometimes you do find real words, even whole text parts inside binary files. If you open a png file it will start with the letters "PNG", or a JPEG contains "JFIF" in its first bytes, or the license text is stored as a whole in an executable.
Some file formats can therefore be identified if seeing certain strings like "BMP" or "RIFF" at the beginning of a file - e.g. if the filename was lost.
Reading Numbers: Byte, Word, Signed, Unsigned?
Now you're already familiar with locating a certain byte position in the file and reading its value - or its interpretation as a text character.
But only numbers from 0 to 255. What about larger numbers? Or negative ones?
Positive/negative numbers (unsigned/signed)
Negative ones are called "signed" in developer terms. That's because we have to sacrifice a whole bit for the "minus sign": sigh
That bit just cost us half of a byte for counting! The maximum of 7 bits is 127. But sometimes you just have to say Goodbye to a bit for it to serve a higher purpose. Sometimes "superfluous" bits, increasing storage size - but offer error correction, sometimes bits to simply "sign" a number.
Negative numbers can also be represented by "inverting" their bit pattern. This is called "two's complement of a signed binary number".
For a proper explanation, more details and how the binary representation of positive and negative numbers look like, please take a look at a nice article about "Signed Binary Numbers" (on "electronicshub.org") or the Wikipedia article about "Two's complement".
Here's an example for a few numbers stored as 8 bit signed integers:
- +7 = 0x07 = 0000 0111
- -7 = 0xF9 = 1111 1001
- +127 = 0x7F = 0111 1111
- -127 = 0x81 = 1000 0001
Therefore in order to interpret the binary data as numbers, you need to know if it's:
- Signed: negative, minus
- Unsigned: positive only
For example:
According to its original specification, a WAV file may not be larger than 2 GB. In almost any file (in a non-streamable format), there's a bunch of bytes that represent the position where the actual "payload data" (e.g. the image, sound, movie, etc) is.
For WAV, this field was defined as 32 bits. This means a maximum payload size of about 4 GB. The reason the actual limit is 2 GB is, that the specification forgot to declare whether these bits were signed or unsigned.
2^32 = 4294967296 = ca. 4 GB
...we lose 1 bit for "maybe it's signed", so:
2^31 = 2147483648 = ca. 2 GB
So in order to play it safe, developers should never create WAV files larger than 2 GB to avoid breaking an implementation that uses 32 bit signed (which is half of 4 GB, due to the "sacrificed" sign bit).
Technically though, it's possible to create 4 GB WAVs. They function properly. IF both ends, encoding and decoding use unsigned 32 bit integer variables.
Word size
If certain bytes (e.g. according to their file format specification - if known) are intended to hold values greater than 255, you also need to know the "word size" of this data field.
A "word" in computer engineering is a data unit. You can encounter different word sizes within one file format. But don't be scared if this sounds a bit complicated.
Let's take another look:
- One byte (8 bit) is max: 0xFF = 255.
- Two bytes (16 bit) are max: 0xFFFF = 65535
- Four bytes (32 bit) are max: 0xFFFFFFFF = 4,294967295e9 = About 4 GB
- Eight bytes (64 bit) = really huge number.
You might recognize these numbers from what you've overheard in tech-media-news:
"Now with 32 bit power!"
And a few years later (that's where we're at now):
"Now with 64 bit power!"
It means their default word size is 32 or 64 bits. So they can crunch larger numbers in one step (="clock tick" of the CPU).
Long story short: More bytes = larger numbers.
In order to read multiple bytes as one single large number, just concatenate as many bytes as required from the binary data and then convert that hex number to decimal.
For example: 0x1234 = 2 Bytes = 4660
Endianess
But there's a little "thing" called "endianess", which is nothing complicated, but can be very nasty. It's: "the sequential order in which bytes are arranged into larger numerical values when stored in memory or transmitted over digital links" (Quote: Wikipedia")
The byte order within a word matters. It makes a difference in which order you concatenate the bytes:
0x1234 is not 0x3412. Obviously.
One way is called "Little Endian" (LE) and the other way is called "Big Endian" (BE). LE is common on PCs (Linux, Windows), whereas BE is common on former Apple hardware (due to a BE CPU architecture).
If you manufacture a glass master for an audio CD, make sure your master image has the endianess matching the hardware of the CD production plant. Otherwise, your mis-matching endianess will end up as hundreds of CDs with just white noise. The data is not gone or corrupted. It's just read the wrong way. If you read such a CD as raw data, and then interpret it in the right Endianess, the audio will be just fine.
It's also possible to convert from little- to big-endian without any data degradation. Lossless so to say. The byte order is just shuffled.
Displaying number values
Most graphical hex editors also offer to display the selected bytes in different ways, as mentioned above: signed/unsigned, little/big endian, different word sizes, etc.
Here's an example of what this looks like in the hex editor called "Bless":
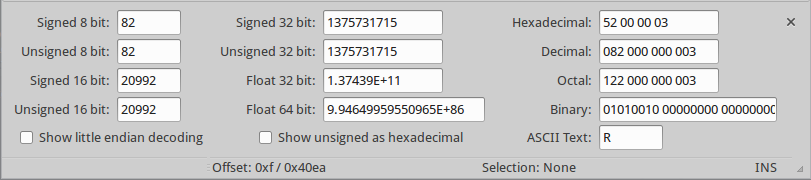
"Different possible ways to interpret numbers/data"
As you can see, it shows the data at the cursor position in different possible ways. The most basic are the first 2 fields (=1 Byte):
- Signed/Unsigned 8 bit
Right below, it shows the numeric values for signed/unsigned with a word size of 2 bytes:
- Signed/Unsigned 16 bit
This way of viewing data is very handy. Especially when reading values like "image resolution" or "samplerate" in a media file.
I didn't have this view option when I first used a hex editor. When I was still a kid, we hex-edited savegames of computer games. For example, when we tried to "hack" how much gold our game character had, it was necessary to copy the hex value from our calculator in the correct endianess-order ;)
Summary
So now, we've explored why handling binary files require a different editor than for text, as well as why a "hex(adecimal)" view of a byte is very useful. Additionally, you should now be able to locate and navigate to certain positions and interpret numeric values, according to data format specifications.
In the next part we'll see how text can be found and edited - even in binary files - and how a a file (like an image- or audiofile) "knows" the technical properties (like resolution, samplerate, etc) of its (media) content - and how to modify such values.
Here is a link to the next part: Hex Editing for Archivists (Part 2) - How to Read & Edit Binary Data
Have a great day! :D